读书笔记:梯度、散度、旋度与麦克斯韦方程组
这一章学习后,主要是记录一下散度旋度的引入对麦克斯韦方程式的进一步的理解。以前主要是从积分形式去定性的理解,个人觉得从散度旋度角度去理解远远比积分形式更深刻。
1、如何理解梯度、散度与旋度
梯度:梯度描述的是场对位置的变化。
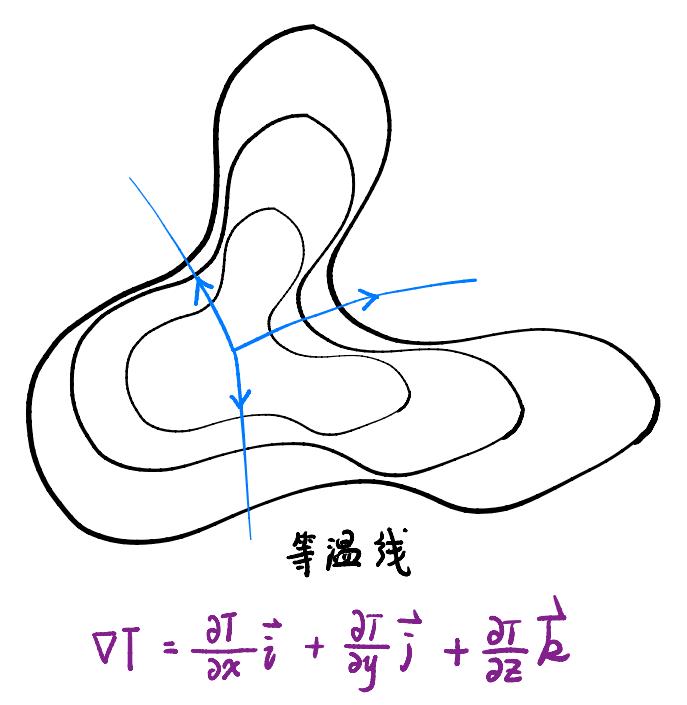
如图所示,对于一个温度场T,我们可以去想象一些等温面,即由温度相等的点构成的一组曲面。将这些曲面分割为无穷小的面积元,该面积元的法线方向就是温度变化最快的方向,数学公式写作:
\[\nabla T=\frac{\partial T}{\partial x} \vec{i} +\frac{\partial T}{\partial y} \vec{j} +\frac{\partial T}{\partial z} \vec{k}\]从上式中,我们可以看出,在计算梯度时,我们的输入是一个标量场,场内每点由单一的数值确定;而它的输出是一个矢量场,描述了场的变化速率与方向。
散度:散度描述的是场单位面积的通量。
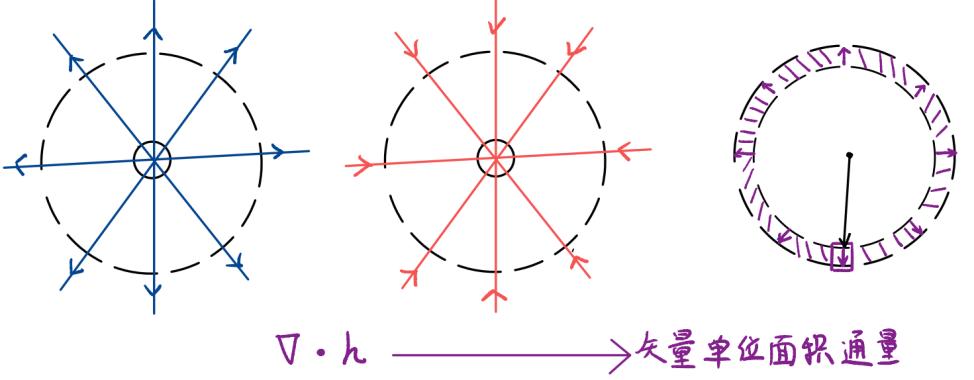
假想一个如上图所示的单位点电荷的电场,对其做一个包围这个电荷的封闭曲面。我们发现所有电场线以净输出(+)或净输入(-)的形式通过这个封闭曲面。如果我们想以定量的形式描述具体有多少电场线净出入这个一定体积的封闭曲面,我们就以散度的数值衡量。它的计算方法是:
\[\nabla \cdot \vec{h}=\frac{\partial h_1}{\partial x}+\frac{\partial h_2}{\partial y} +\frac{\partial h_3}{\partial z}\]散度是一个很好的判断发射源或吸收源的方式,它帮助我们描述一个场的场源。从公式中,我们可以看出,散度的输入是一个矢量场,具有数值与方向,而它的输出为矢量通过封闭曲面的通量,即闭曲面通量体密度,是标量场。定义为:
\[div \ \vec{h} =\lim_{\bigtriangleup V \to 0} \frac{\oint _s \vec{h}\cdot \vec{n} dS}{\bigtriangleup V}\]旋度:旋度描述一个场单位面积的环量。
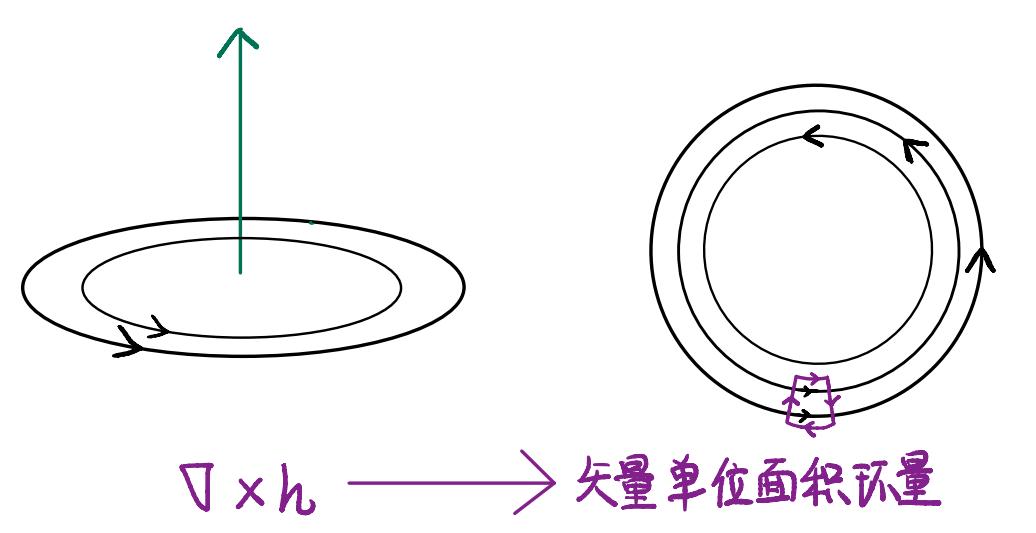
我们再次将一个场划分为无穷小的面积元,这一次我们取这个面积元的边框,并尝试计算顺时针环绕该面积元的量,这样我们就得到了场在这一位置的旋度,计算方式为:
\[\nabla \times \vec{h} =\begin{vmatrix} \vec{i} & \vec{j}& \vec{k}\\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y}& \frac{\partial}{\partial z}\\ h_1 & h_2 & h_3 \end{vmatrix}\]这一公式的输入和输出都是矢量场,输出场的方向为面积元的法向方向,其大小为单位曲面的环量,即闭曲线环量的面密度。定义为:
\[\vec{n} \cdot rot \ \vec{h} = \lim_{\bigtriangleup S \to 0} \frac{\oint_{L} \vec{F}\cdot d\vec{L}}{\bigtriangleup S}\]梯度无旋:\(\nabla \times (\nabla \vec{h})=0\)。一个梯度场的场线,永远指向其场的正变化方向,由此容易推得如果一个梯度场的场线首尾相连成环状等效于场变化量为零,该场不存在,所以梯度场不会出现净环量,故梯度无旋。
旋度无散:\(\nabla \cdot (\nabla \times \vec{h})=0\)。一个旋度场的场线成环状,单位体积场线出入量相等,无净通量,场内并不会表现出发射状或吸收状场源,故旋度无散。
拉普拉斯算符
拉普拉斯算符等效为一个场关于空间的二阶微分算符,记为:\(\bigtriangledown ^2=\frac{\partial^2}{\partial x^2} +\frac{\partial^2}{\partial y^2} +\frac{\partial^2}{\partial z^2}\)。
这是一个标量算符,当我们将它作用于一个标量场时,得到一个标量场:\(\nabla \cdot (\nabla T)=\bigtriangledown ^2 T=标量场\) 。
当我们将它作用于一个矢量场时,得到一个矢量场:\((\nabla \cdot \nabla) \vec{h} =\nabla ^2 \vec{h} =矢量场\)。
2、麦克斯韦方程组
麦克斯韦方程组:
I.\(\nabla \cdot E = \frac{\rho }{\varepsilon _0}\);(穿过一闭合面的E通量)=(面内电荷密度)/\(\varepsilon _0\)。
II.\(\nabla \times E = -\frac{\partial B}{\partial t}\);(E环绕一回路的积分)=\(-\frac{\partial }{\partial t}\)(穿过该回路的B通量)。
III.\(\nabla \cdot B=0\);(穿过一闭合面的B通量)=0。
IV.\(c^2\nabla \times B=\frac{j}{\varepsilon _0} +\frac{\partial E}{\partial t}\);\(c^2\)(B环绕一回路的积分)=(穿过该回路的电流)/\(\varepsilon _0\)+\(\frac{\partial }{\partial t}\)(穿过该回路的E通量)
电荷守恒:\(\nabla \cdot E = -\frac{\partial \rho}{\partial t}\)
力的定律:\(F=q(E+v \times B)\)
涉及到经典电磁学的问题能很好地用上述方程组表述。
第一个方程与第三个方程容易理解。对于方程I,散度仅与其场源相关,即穿过任何闭合面的E通量与面内电荷成正比。无论对于静态场或动态场,高斯定律永远正确。对于方程III,自然界没有单独的磁荷存在,即磁场不像电场,没有可以单独作为场源的物质存在,其散度永远为零。
方程II表明,一个随时间变化的磁场,会导致一个电场的环流,产生一个与磁场变化方向相反的量去阻止这一变化。
对于方程IV,我们需要进一步推敲。根据旋度无散,我们知道,如果对等式左侧计算散度,它一定为零。同样地,我们对等式右侧也求散度,得到:
\[\nabla \cdot \frac{j}{\varepsilon _0} + \nabla \cdot \frac{\partial E}{\partial t}=0\]电荷守恒公式表明,电荷不会凭空产生,任何一处电荷的流出等于某处电荷密度的减少。显然这一项没有必要为零,因为电荷密度可以随时间变化,所以为了使等式成立,我们添加了一个补偿项\(\nabla \cdot \frac{\partial E}{\partial t}\)。 在补偿项中,我们带入高斯定律,用电场场源电荷随时间的变化,与电流散度项相对应。于是,我们得到了完备的方程IV。
方程II与方程IV揭示了一些有趣的现象:若一个变化的磁场产生了电场,在这个电场试图消逝时,它又会因变化的电场激发出磁场,通过如此往复,由一个场到另一个场,这就构成了穿越空间传播的电磁波。根据方程IV的积分形式:
\[c^2\oint_{\Gamma _1}^{} B\cdot dL=\frac{d}{dt} \int_{\Gamma _1}^{}E \cdot \vec{n} ds\]而E通量的变化率仅仅由电磁波波前引起,可以得到:
\[c^2 B=Ev\]3、矢势、标势
根据方程III和旋度无散,我们推得B是某个量的旋度,记为:\(B=\nabla \times A\),称为矢量势A。
将我们的推论带入方程II:\(\nabla \times (E+\frac{\partial A}{\partial t} )=0\)。
根据梯度无旋,我们推得\(E+\frac{\partial A}{\partial t}\)是某个量的梯度,记为:\(-\nabla \phi= E+\frac{\partial A}{\partial t}\),\(\phi\)称为标量势。
如何从物理意义上理解矢势与标势?
首先我们先从图形上领会矢势。如图是圆电流和直电流的B与A。
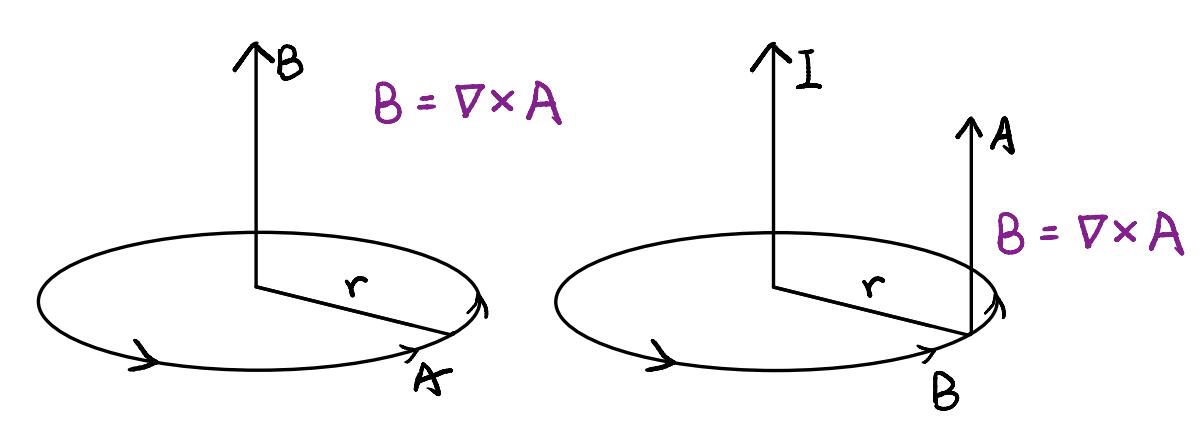
从方向上,A与电流I有相同的方向。这其实从A的定义上能推得,因为A的旋度方向为B,而B的旋度方向又为I。在运算中,A类比于I。
从毕奥-萨伐尔定律对A与B的通解能很好地明确这两个量的关系:
\[B(1)=\frac{1}{4\pi \varepsilon _0 c^2} \int \frac{j(2)\times e_{12}}{r_{12}^2} dV_2\] \[A(1)=\frac{1}{4\pi \varepsilon _0 c^2} \int \frac{j(2)}{r_{12}^2} dV_2\]也就是说,B与方向r单位向量的叉积就是A。鉴于B方向垂直于I,sin90=1,将B转至与I相同的角度就可以得到A。
而对于标势\(\phi\),根据其公式形式\(-\nabla \phi= E+\frac{\partial A}{\partial t}\),我们可以推测出这里的标势应该类比于单位体积电荷量,其梯度为电荷量的变化速度最快的方向,\(E\)表征电荷量的空间变化,而\(\frac{\partial A}{\partial t}\)表征电荷量的时间变化,而且其方向由B方向矫正为A,与E方向一致,便于进行叠加。
关于矢势与标势更进一步的学习会在量子力学中继续,这里我们只是浅浅讨论一下。
参考书籍:《费曼物理学讲义》