读书笔记:由加速电荷推导出的电磁波性质(光传播的经典理论)
这一章节知识点比较宽泛,感觉有点杂  ̄﹏ ̄,所以觉得有系统整理的必要。有部分知识点并没有进行详细讨论,但在未来的章节应该会提及,所以暂且跳过讨论部分只给出结果。在分析这一章的内容时,我们注意到为了简化问题,多处取了近似情况进行分析。以后运用它们分析实际问题时,也要特别注意这些特殊近似条件。
1 加速电荷产生的场
首先,书中给出了由一个单独电荷产生的电场在某一点P的表达式:
\[E=-\frac{q}{4\pi \varepsilon _{0}}[\frac{e_{r'}}{r^{'2}}+\frac{r'}{c}\frac{d}{dt}(\frac{e_{r'}}{r^{'2}})+\frac{1}{c^{2}}\frac{d^{2}e_{r'}}{dt^{2}}]\]式中,\(r’\)表示现在到达P的信号,在从电荷出发时与P点的距离。这个公式的推导还是要等后面进入场的学习的时候进一步思考,现在我们只是单纯分析这一公式所导出的结果。显然在上式的诸多项中,第一项与第二项都是随着距离的平方衰减的项,而第三项随距离的一次方衰减。当距离足够远时,第三项是唯一重要的项:
\[E=-\frac{q}{4\pi \varepsilon _{0}c^{2}} \frac{d^{2}e_{r'}}{dt^{2}}\]现在我们把它应用于一种更简单的情况:电荷运动的速度不大。这样,\(r\)的改变量很小,\(r\)近似不变,所以延迟时间也就不变。上式就可以写成:
\[E=-\frac{q}{4\pi \varepsilon _{0}c^{2}} \frac{d^{2}}{dt^{2}}[\frac{x(t-r/c)}{r} ]=-\frac{q}{4\pi \varepsilon _{0}c^{2}}[\frac{a_{x} (t-r/c)}{r} ]\]如下图所示,式中只有横向分量是重要的,因为其尾端上下运动,而径向分量则停留在球面上。 所以我们进一步将公式提取如下:
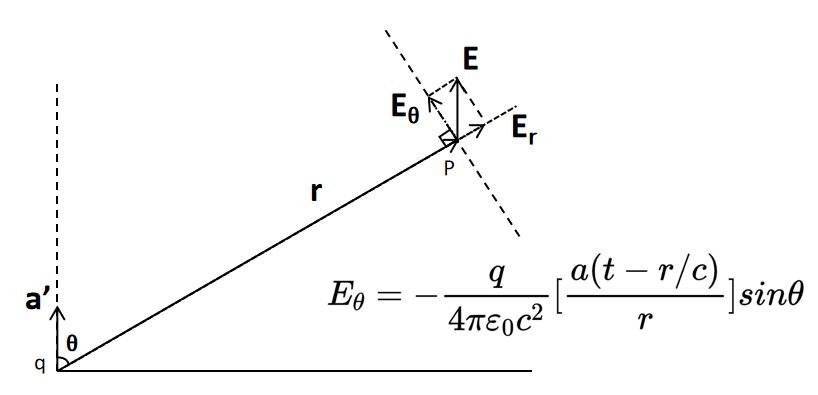
其实在这里,我们建立的这个粗略的电磁波传播的模型已经暗示了一个有趣的现象:一束电矢量方向确定的非偏振光,照射到原子上后,我们在与入射光成90度的方向观察原子的散射光,这束光是偏振的!因为一个受激振子朝着我们或背离我们振动,我们是看不见的;只有横向的振动能够传播过来。这也很好地解释了布儒斯特角的原理!当反射光与折射光夹角成90度时,反射光是完全偏振光,其偏振方向垂直于反射光与折射光组成的平面。
2 振荡电荷组成的平面的场
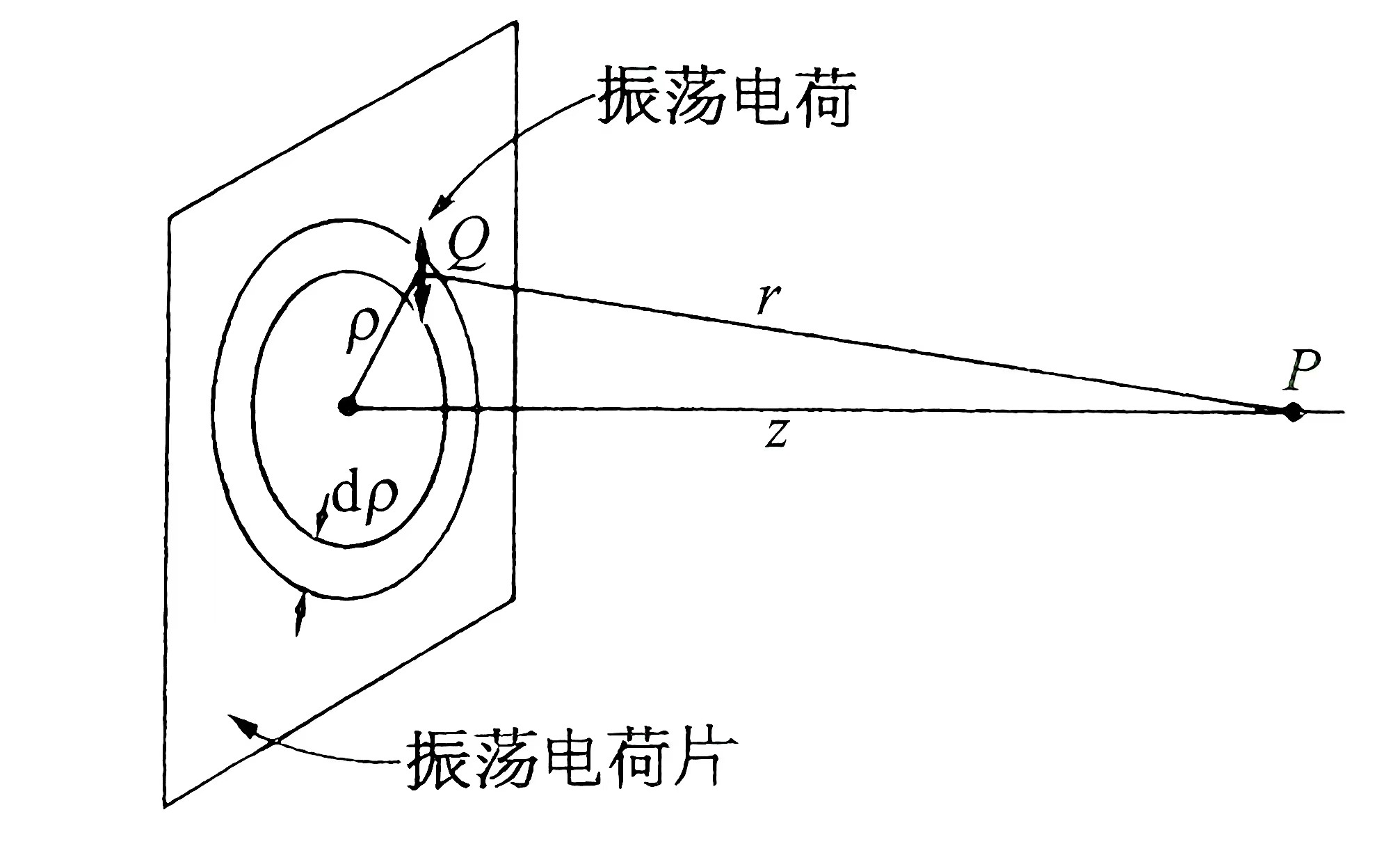
如图所示,上述电荷组成一个电荷片平面,平面上单位面积的电荷数量是\(\eta\),所有电荷做同方向、同振幅、同相位的简谐振动:\(x=x_{0}e^{i\omega t}\),\(a=-\omega ^{2} x_{0}e^{i\omega t}\)(要特别习惯复数与三角函数的替代分析,这往往能简化很多问题;只要虚数的引入不为实部引入新的量,我们就认为这两种分析是等价的)。当波传播到距离平面为\(z\)的P点时:\(a(t-r/c)=-\omega ^{2} x_{0}e^{i\omega (t-r/c)}\)
当P点与平面相距足够远时,\(sin \theta \approx 1\):\(E_{\theta} \approx \frac{q}{4\pi \varepsilon _{0}c^{2}} \frac{\omega ^{2} x_{0}e^{i\omega (t-r/c)} }{r}\)。
我们对全平面进行积分:
\[E=\int_{\rho =0}^{\rho =\infty} \frac{q}{4\pi \varepsilon _{0}c^{2}}\frac{\omega ^{2} x_{0}e^{i\omega (t-r/c)} }{r} 2\pi \eta\rho d\rho\]因为\(r^{2} =\rho ^{2} +z^{2}\),所以\(2rdr=2 \rho d \rho\)。
\[E=\frac{q \omega ^{2} x_{0} e^{i\omega t} }{2 \varepsilon _{0}c^{2}}\eta \int_{r =z}^{r =\infty} e^{-i\omega r/c} dr=\frac{q \omega ^{2} x_{0} e^{i\omega t} }{2 \varepsilon _{0}c^{2}}\eta [-\frac{c}{i\omega }(e^{-i\infty }-e^{-i\omega z/c})]\]从数学上看这个积分并不复杂。但是书中给出了非常非常有趣的几何分析方式,让这个数学问题的物理意义突然变得立体了起来!所以我在这里特别想记录一下:
如图所示:
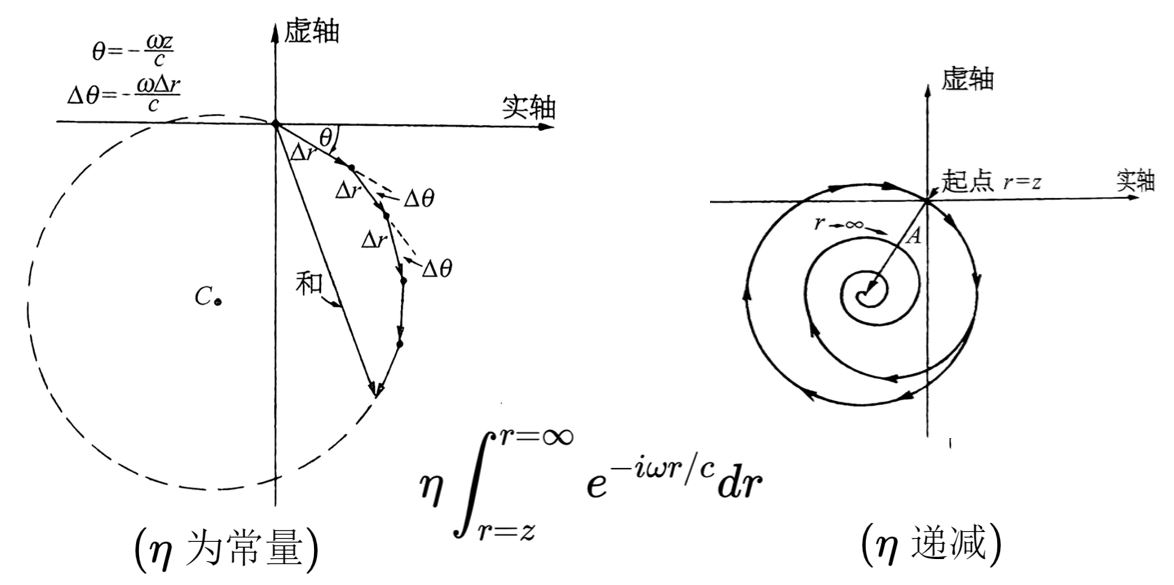
当\(\eta\)为常数时,这一积分过程等效于相同的模长的向量,以相同的辐角增量首尾相接。其趋于无穷大的结果必然是在这一圆上的循环,没有确切的解。但真实世界中,不可能存在无限大的平面,电荷在某一区域必然触及边缘使密度下降,这时\(\eta\)必然逐渐缩小。所以在图中表现为模长逐渐减小的向量,以相同的辐角增量收尾相接,形成螺旋线,收敛至圆心。其结果恰好是上面数学解的\(e^{-i\infty }\)项为0。我们得到:
\[E=\frac{q \omega ^{2} x_{0} e^{i\omega t} }{2 \varepsilon _{0}c^{2}}\eta (\frac{c}{i\omega }e^{-i\omega z/c})=\frac{q \eta }{2 \varepsilon _{0}c} i\omega x_{0} e^{i\omega (t- z/c)}\] \[E=\frac{q \eta }{2 \varepsilon _{0}c} v(t- z/c)\]有趣的是,书中提及,上式我们是由距离\(z\)足够大这一条件推导而来的,但上述公式却适用于任意距离\(z\),包括\(z < \lambda\)。
补充:衍射光栅
衍射与干涉的知识与前文相比还是好理解的,这一块不准备细讲,但是还是想提醒自己时刻保持图解法分析问题的意识。以衍射光栅的分辨能力问题为例:当N条刻痕的光线矢量图收尾相接刚好转过\(2 \pi\)时,有最小的光强,即\(\lambda =Nd sin\theta\)。所以光栅的分辨本领为\(R=\lambda/\bigtriangleup \lambda =kN\)。
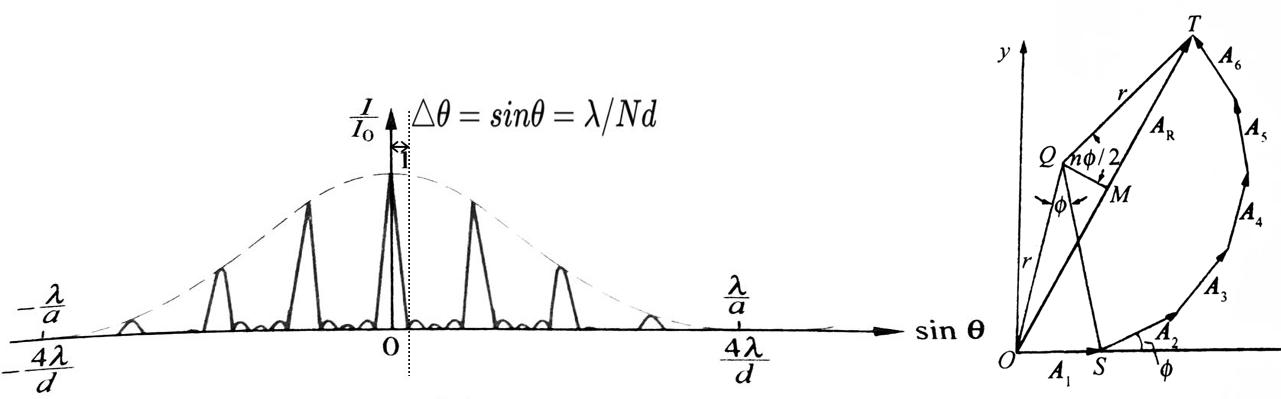
干涉和衍射的本质就是不同光程差造成的相位差的叠加。每一列波可以看成模长为振幅,方向为相角的矢量。如上图所示的图解法能很好的帮助我们求解衍射的强度。
3 物质引起的场与折射现象
以前,在学习中,主要是从宏观上去理解折射现象,在进一步分析由“场”引起的折射之前,我们先来回顾一下。如图:
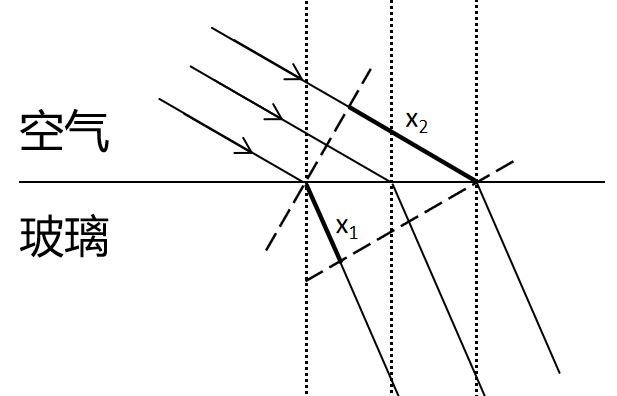
显然,为了保证光束的波阵面进入介质后仍然保持一致,通俗地说就是“一起传播”,光在光程\(x_{1}\),\(x_{2}\)上,必然有相同的耗时。即,折射现象告诉了我们光在介质中改变了自己的速度。上图中,光在玻璃中的传播速度显然慢于空气。光在介质中的传播速度为:\(v=c/n\)。
现在我们想进一步分析造成这一现象的原因:为什么光在不同的材料中表观波速度不同?
根据以前所述的原理,远离所有运动电荷的任意一点电场是光源产生的场与玻璃板中,每个电荷产生的场的矢量和,每个场的延迟速度为\(c\)。
我们已知的场是由光源产生的,它的表达式为:\(E_{s}=E_{0}e^{i\omega (t-z/c)}\)。
我们想要知道的场是玻璃板引入的场。通过观察折射现象,可以知道通过玻璃板后的光场。假设玻璃板厚度为\(\bigtriangleup z\),通过这一玻璃板造成的延时为\(\bigtriangleup t=(n-1)\bigtriangleup z/c\)。所以我们在板后的光场中补入这一延时:
\[E_{板后} =E_{0} e^{i\omega (t-z/c)} \times e^{-i\omega (n-1)\bigtriangleup z/c}\]于是,我们发现,板的效果实际上式相对于场乘上了一个相位因子。但我们更希望写成附加的形式来独立地分析玻璃引入的场,所以,\(\bigtriangleup z\)非常小时,我们把附加的相位因子改写成如下形式:
\[e^{-i\omega (n-1)\bigtriangleup z/c}=1-i\omega (n-1)\bigtriangleup z/c\]于是,带入到板后的公式,我们得到:
\[E_{板后} =E_{0} e^{i\omega (t-z/c)}-\frac{i\omega (n-1)\bigtriangleup z}{c} E_{0} e^{i\omega (t-z/c)}\]第一项是光源的场,第二项显然就是玻璃板引入的光场了:\(E_{a}=-\frac{i\omega (n-1)\bigtriangleup z}{c} E_{0} e^{i\omega (t-z/c)}\)。我们用图解的方式能更好的理解玻璃板的作用。显然玻璃板是让光源\(E_{s}\)在复平面上转过了一个负的角度!
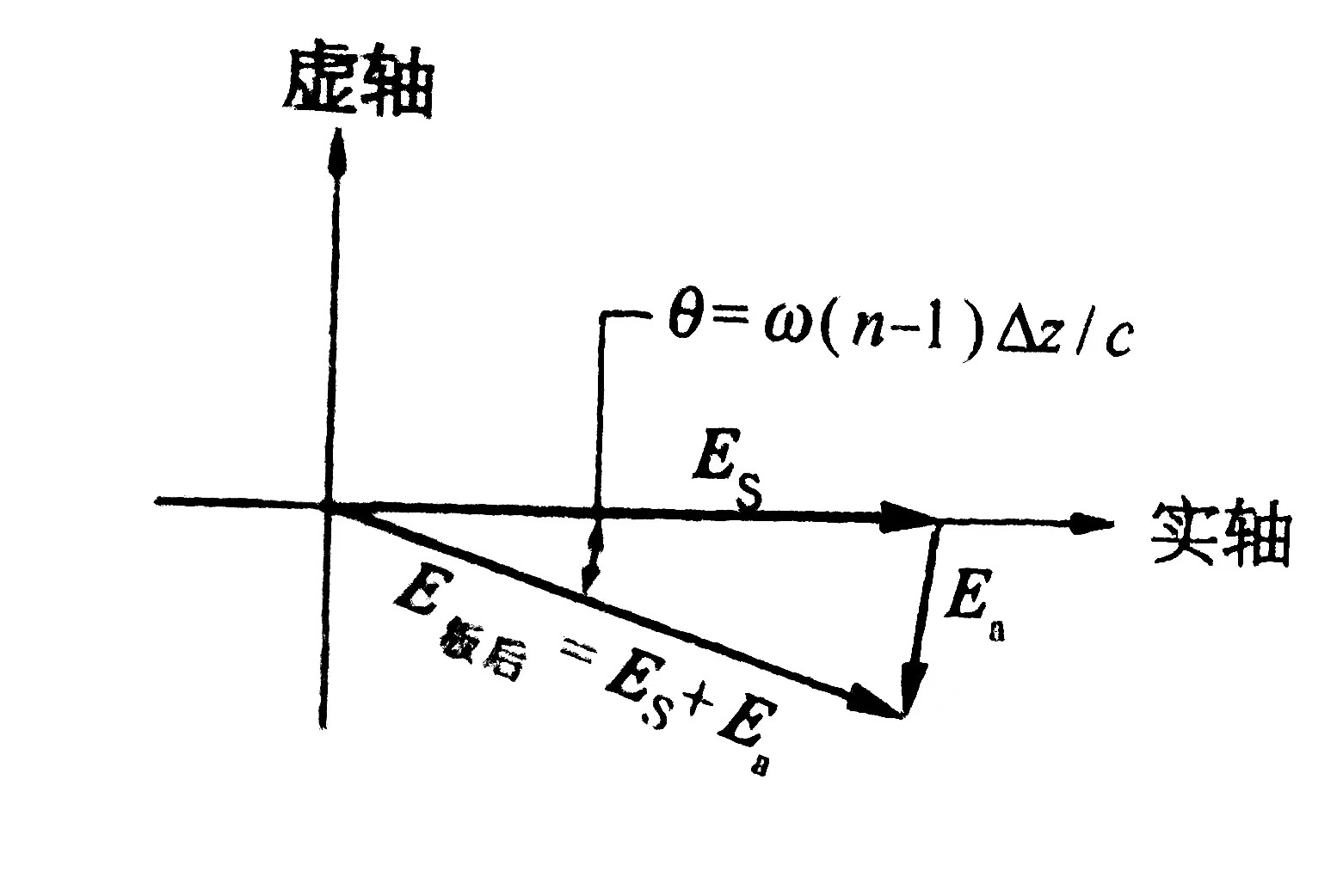
现在,我们已经有了一个介质引入的场的表达式\(E_{a}\),但是我们还想更进一步,因为式中还是有一个非基本量,折射率\(n\)。我们希望能够从材料的特性中,将这个\(n\)求解出来。所以我们换一个思路考虑这个问题。
电子在原子中的行为,可以假设为被弹簧拴着的小振子,共振频率为\(\omega _{0}\)(这一模型参考波动力学理论),有如下方程:
\[m(\frac{\mathrm{d}^{2} x}{\mathrm{d} t^{2}}+\omega _{0}^{2}x)=qE_{0}e^{i\omega t}\]这一方程我们在前面的笔记里已经写得超详细了,以下的振子模型相关的问题就全部直接上结果啦。这一振子的运动方程的解为:
\[x=\frac{qE_0}{m(\omega _0 ^2-\omega ^2)} e^{i\omega t}\]我们现在把这一结果带入到第二节我们得到的与振荡电荷片相距为\(z\)的合场强的计算公式里去:
\[E_{a}=\frac{q \eta }{2 \varepsilon _{0}c} v(t- z/c)=\frac{q \eta }{2 \varepsilon _{0}c}[i\omega \frac{qE_0}{m(\omega _0 ^2-\omega ^2)} e^{i\omega (t-z/c)}]\]我们现在有两个\(E_{a}\)的表达式了!联立起来得到折射率的表达式:
\[n=1+\frac{Nq^{2} }{2\varepsilon _0 ^{2}m(\omega _0 ^2-\omega ^2)}\]式中,\(\eta = N \bigtriangleup z\)。
4 电磁波的色散与吸收
折射率取决于频率的现象成为色散现象。上一节中,我们得到的折射率方程就是色散方程。但是这一方程是简略后的情形。首先,振子的模型必有一定的阻尼力;其次,对一特定种类的原子有几个共振频率。假设单位体积中有\(N _{k}\)个自然频率是\(\omega _{k}\)、阻尼系数是\(\gamma_{k}\)的电子,这样色散方程就成为:
\[n=1+\frac{q^{2} }{2\varepsilon _0 ^{2}m}\sum_{k}^{}\frac{N_k}{\omega_k ^2-\omega ^2+i\gamma _k\omega }\]当自然频率\(\omega _{k}\)远大于\(\omega\)时,我们发现折射率近似为常数,例如大多数气体的折射率。当\(\omega\)增大时,折射率也会增大,所以光线会弯折的更厉害。对于X射线来说,它比绝大多数材料的共振频率高,所以其折射率都略小于1;这些材料对X射线都是透明的。
折射率小于1要如何理解?它表示光速大于1吗?其实这里的速度我们指的是相速度。相速度不能传播信息,它暗示了电荷振动的相位与策动场不同。相速度大于光速的波,其相位是超前的,但是波本身(即波的起始端点)并不会提前到达。
从我们的色散方程可以看到,我们引入了阻尼项\(i\gamma\)。在受迫振动的分析中,我们已经提到过,阻尼项就是能量的吸收项。也就是说,复折射率的虚部就是波的吸收。从前一节\(E_{a}\)的图中,我们也可以看出穿过玻璃后\(E_{s}+E_{a}\)的实部变小了。这就是透射场减弱的原因。
当自然频率\(\omega _{k}\)十分接近\(\omega\)时,折射率几乎完全变为虚部,光的吸收变为占优势的效应。
5 电磁波的能量、辐射阻尼与原子的谱线宽度
在前文中,我们已经说明了电磁波的吸收与散射可以等效为一个受迫振子的行为,其能量消耗在阻尼项\(i\gamma\)项上,我们称之为辐射阻尼。显然,这一振动系统有对应的阻力\(\gamma\)与Q值。求解出了这些值,我们就能得知原子的共振谱线!
在此之前我们来分析电磁波所携带的能量。首先,我们知道场强E正比于光的振幅A,所以光所携带的能量正比于\(E^2\)。这里,我们定义一个比例系数\(\alpha\)。
我们知道对于介质来说:每秒流入能量=每秒流出能量+每秒做功。所以(略去高阶无穷小量):
\[\alpha \overline{E_{s}^{2}} = \alpha \overline{(E_{s}+{E_{a})^2}}+N\bigtriangleup zq\overline{E_s v}\approx \alpha \overline{E_{s}^{2}}+2\alpha \overline{E_s E_a} +N\bigtriangleup zq\overline{E_s v}\] \[2\alpha \overline{E_s E_a} =-N\bigtriangleup zq\overline{E_s v}\]已知\(E_a=\frac{q N\bigtriangleup z }{2 \varepsilon _{0}c} v\),带入上式中,得到:
\[\alpha = \varepsilon _0 c\]所以我们能得到电磁波强度公式:
\[\overline{S} = \varepsilon _0 c \overline{E^2}=能量/面积/时间\]我们现在把前面推导的公式全部结合起来,原子的谱线宽度问题就迎刃而解了!
\[\begin{cases}E_\theta =-\frac{q}{4\pi \varepsilon _{0}c^{2}}[\frac{a(t-r/c)}{r} ]sin\theta \\ \\\overline{S} = \varepsilon _0 c \overline{E^2}\approx \varepsilon _0 c \overline{E_\theta ^2} = \frac{q^{2} a^{'2}sin^2\theta}{16\pi ^2\varepsilon _0 r^2 c^3} \\ \\W=\frac{1}{2} m\omega _{0}^{2}x^{2} \\ \\P=\int SdA = \frac{q^{2} a^{'2}}{6\pi \varepsilon _0 c^3} =\frac{q^2\omega _0 ^4}{12\pi \varepsilon _0c^3} x^2 \\ \\Q=\frac{W}{dW/d\phi }=\frac{\omega _0 W}{dW/dt}=\frac{\omega _0 W}{P}=\frac{\omega _{0} }{\bigtriangleup \omega }=\frac{\omega _0}{\gamma } \\ \\\bigtriangleup \lambda =\frac{2\pi c\bigtriangleup \omega}{\omega _0 ^2} =\frac{\lambda }{Q} \end{cases}\]解得:
\[Q=\frac{3\lambda }{4\pi r_0} , r_0=\frac{q^2}{4\pi \varepsilon _0mc^2}\] \[\gamma = \frac{\omega _0}{Q} =\frac{2r_0\omega _0^2}{3c}\] \[\bigtriangleup \lambda =\frac{\lambda }{Q}=\frac{4\pi r_0}{3}\]6 光的散射与普朗克黑体辐射公式
在上一节的受激振子模型中,我们主要分析了阻尼项\(i\gamma\)项导致的强吸收谱线。但对于其他吸收不强烈的情况,原子作为一个散射源,而能量被辐射出去。我们在这一节中,重点分析光的散射现象。
上一节中,我们给出了辐射功率的公式:
\[P=\int SdA = \frac{q^{2} a^{'2}}{6\pi \varepsilon _0 c^3} =\frac{q^2\omega ^4}{12\pi \varepsilon _0c^3} x^2\]总散射功率对应于受激振子在单位时间向所有方向辐射出的能量的总和,也就是电磁波强度在球面的积分。振子的模型还是沿用之前的公式:
\[\hat{x}=\frac{q\hat{E_0} }{m(\omega _0 ^2-\omega ^2+i\omega \gamma )}\]代入散射功率的公式:
\[P =(\frac{q^2\omega ^4}{12\pi \varepsilon _0c^3}) x^2=(\frac{q^2\omega ^4}{12\pi \varepsilon _0c^3})[\frac{q^2 E_0 ^2 }{m^2(\omega _0 ^2-\omega ^2+i\omega \gamma )^2}]\] \[=(\frac{1}{2} \varepsilon _0 c E_0 ^2)(\frac{8\pi r_0^2}{3})[\frac{\omega ^4}{(\omega _0 ^2-\omega ^2)^2+\gamma ^2\omega ^2} ]\]公式经过整理后,我们发现各个方向散射的总功率等于入射电磁波强度乘以一个面积,我们将这个面积称为散射截面\(\sigma _s\)。这并不是说振子有一个物理意义的面积,而是为了表征散射功率与入射电磁波强度的比值,是一种分析方式。
\[\sigma _s=\frac{8\pi r_0^2}{3}[\frac{\omega ^4}{(\omega _0 ^2-\omega ^2)^2+\gamma ^2\omega ^2}]\]上面我们已经根据一个受迫振动的电荷模型计算出了它的能量吸收(辐射阻尼)与辐射(散射)情况,现在我们来思考一些更复杂的情景。在一个达到热平衡(即单位时间从物体表面辐射的电磁波量与吸收的电磁波量相等)的封闭容器中,单位时间散射的总能量为所有频谱的电磁波强度与等效散射截面相乘:
\[\frac{dW_s}{dt} =\int_{0}^{\infty} I(\omega )\sigma _s(\omega )d\omega =\left \langle E \right \rangle\]注意\(\gamma =\frac{2r_0\omega _0^2}{3c}\)。
这里不详细解方程了,给出结果:\(I(\omega )=\frac{\omega ^2\left \langle E \right \rangle}{\pi ^2 c^2}\)。平均能量\(\left \langle E \right \rangle\)的取值正是由经典物理走向量子物理的起点!
在经典物理学中,每个自由度的能量取值为:\(\left \langle E \right \rangle=kT\)。而由这一结果导出的公式显然与实际不符,是荒谬的。
而量子振子理论给出的能量应该为:\(\left \langle E \right \rangle=\frac{E_总}{N_总}=\frac{N_0\hbar \omega (0+p+2p^2+3p^3+...)}{N_0(1+p+2p^2+3p^3+...)}=\frac{\hbar \omega}{e^{\hbar \omega/kT}-1}\),其中 \(p\) 是每上升一个能级该能级粒子概率的变化系数:\(p=e^{-\hbar \omega/kT}\)。
于是我们得到了第一条量子力学公式,即普朗克黑体辐射公式:
\[M_\nu =\frac{2\pi h}{c^2} \frac{\nu ^3}{e^{h\nu /kT}-1}\]参考书籍:《费曼物理学讲义》、《大学物理学》(张三慧)