Z变换的理论基础
最近常常接触到数字信号处理的相关知识,发现自己以前学的都忘得差不多了(ó﹏ò。)。借此机会整理一下这门课的知识点,以后也能常常翻阅。这一篇主要是回顾z变换的相关知识。
1 Z变换与离散傅里叶变换
傅里叶变换是日常必备的基础知识之一。把傅里叶变换作为切入点能很好地理解其他变换的数学特点。我们先来看看Z变换和离散傅里叶变换的公式:
\[X(z)=\sum_{n=-\infty }^{\infty} x(n)z^{-n}\] \[X(e^{j\omega } )=\sum_{n=-\infty }^{\infty} x(n)e^{j\omega n}\]n指第n次采样的数值。显然,离散傅里叶变换就是将\(z\)替换为了\(e^{j\omega }\),即离散傅里叶变换是z变换的特例。而离散傅里叶变换就是系统在单位圆上的采样,如下图所示。\(0\)到\(2\pi\)是频率,而每个点的采样值构成其幅度谱。
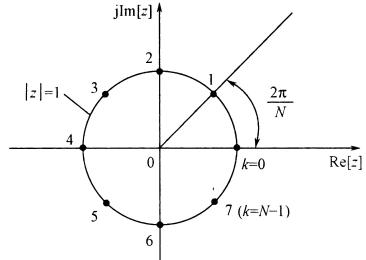
以上这些都是能在课本上轻易找到的知识点,但看完还是容易疑惑。有了离散傅里叶变换为什么还需要Z变换?Z变换究竟延拓了什么?既然说是延拓,那么Z变换必然能够解决离散傅里叶变换不能解决的问题。那么什么情况下,离散傅里叶变换不适用呢?
其实任何变换都应该满足绝对可和,即幂级数必须收敛,变换才是有意义的。而对于无限长的序列,离散傅里叶变换未必满足该条件,所以我们给序列加一个衰减项\(e^{-\alpha n}\),即信号随采样次数指数衰减。于是得到:
\[z^{-n} =e^{-(\alpha+j\omega ) n}\]衰减项变为0的时候,就有了离散傅里叶变换。此外,Z映射到S域就有了拉普拉斯变换(\(z^{-n} =e^{-sTn}\))。但是鉴于我Z变换的相关知识就已经回忆的很艰难了(′へ`、 ),这次就不讨论拉普拉斯变换相关知识了。
2 Z变换的收敛域
收敛域,顾名思义是Z变换在Z平面满足幂级数收敛的区域。
首先,对于有限长输入序列\(x(n)\),显然收敛域为\(0 <abs(z)<\infty\)。(右边序列不包含\(z=0\);左边序列不包含\(z=\infty\))
对于无限长序列,涉及到的都是高数里比较浅显的幂级数收敛的知识,这里就不讲得太细了。直接说结论:
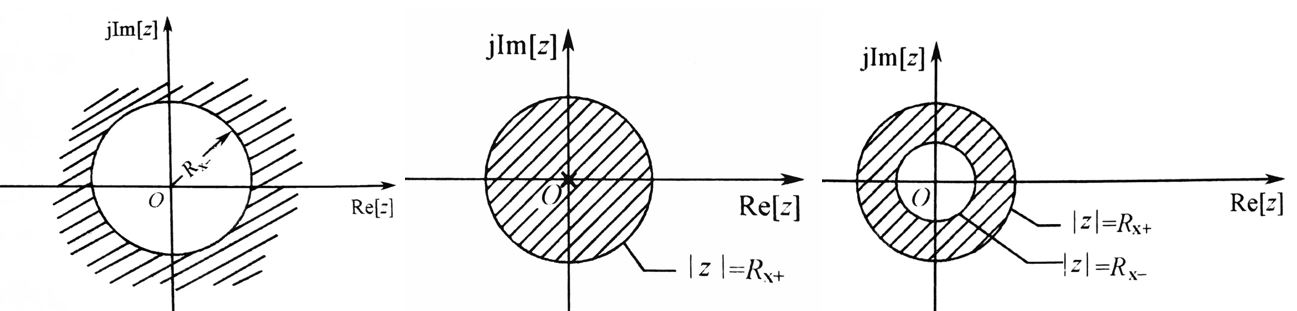
(1)对于右边序列,拆解为一个有限长左边序列和无限长右边序列。收敛域为:\(R_{x-} < abs(z) <\infty\)(因果序列不包含左边有限长序列,故\(R_{x-} < abs(z) \le \infty\))。
(2)对于左边序列,拆解为一个有限长右边序列和无限长左边序列。收敛域为:\(0<abs(z)<R_{x+}\)(若不包含右边有限长序列,则\(abs(z)<R_{x+}\))。
(3)对于双边序列,如果存在,取无限长右边序列和无限长左边序列的交集。
3 Z变换的单位圆与系统的零极点
首先,先看系统函数的定义:
\[H(z)=\sum_{n=-\infty }^{\infty}h(n)z^{-n}\]如果用输入输出表达则有(注意这里涉及到分子分母的多项式因式分解):
\[H(z)=\frac{Y(z)}{X(z)}=\frac{\sum_{m=0}^{M}b_{m}z^{-m}}{\sum_{k=0}^{K}a_{k}z^{-k}}=K\frac{\prod_{m=1}^{M}(1-c_{m}z^{-1} ) }{\prod_{k=1}^{N}(1-d_{k}z^{-1})}\]式中,\(X(z)\)和\(Y(z)\)分别是系统的输入和输出。如果\(h(n)\)是稳定的,即满足绝对可和,那么系统函数的收敛域必然包含\(1 \le abs(z)\le \infty\)。换言之,因果稳定系统的系统函数的全部极点必在单位圆内。
其实这句话很好理解。别忘了,Z变换是我们将离散傅里叶变换加上衰减项\(e^{-\alpha n}\)延拓来的。当\(\alpha >0\)时(极点在单位圆外),Z变换是靠我们运算中附加的指数衰减项才收敛的;而实际系统并不存在这一项。也就是说系统无法收敛,其输出必然发散。
接着,讨论系统的频率响应时,我们回到离散傅里叶变换,此时没有附加的衰减项,是系统最原本的状态,即\(H(e^{j\omega } )\)。
频率响应的幅度谱为不同频谱分量\(\omega\)对应的模,即\(abs(H(e^{j\omega } ))\)。频率响应的相位谱为不同频谱分量\(\omega\)对应的角度,即\(\theta (\omega )=arg[H(e^{j\omega } )]\)。这里,顺便提一句线性相位,满足\(\tau (\omega )=-\frac{d\theta (\omega )}{d\omega }\)为常数的系统就是线性相位系统。\(\tau (\omega )\)是系统的群延时,群延时为常数,表明该系统的输入输出相位只是依次滞后一个常量,容易补偿和恢复;而非线性相位则容易畸变。
4 全通系统和最小相位系统
全通系统顾名思义信号全部通过,频率响应的幅度恒为常数:\(abs(H(e^{j\omega } )) \equiv A\)
由上面这个式子,我们可以猜想一下,这个系统函数除去比例系数\(K\)后的分子分母应该是什么关系?考虑到公式\(H(z)=K\frac{\prod_{m=1}^{M}(1-c_{m}z^{-1})} {\prod_{k=1}^{N}(1-d_{k}z^{-1})}\),我们能给出几个猜测:(1)零极点存在且数量相等,且极点在单位圆内;(2)零极点的模相等使幅度值稳定(3)零极点的单位圆的频率响应的自变量\(e^{j\omega}\)会相互抵消。
所以我们可以发现,全通系统的零点和极点拥有相同的虚部\(e^{j\omega}\),且实部共轭使模完全相等,即\(abs( \alpha + j\omega)= abs(- \alpha + j\omega)\)。所以z变换如图,零点的指数的幂的实部是极点的倒数,但辐角\(\omega\)相等。
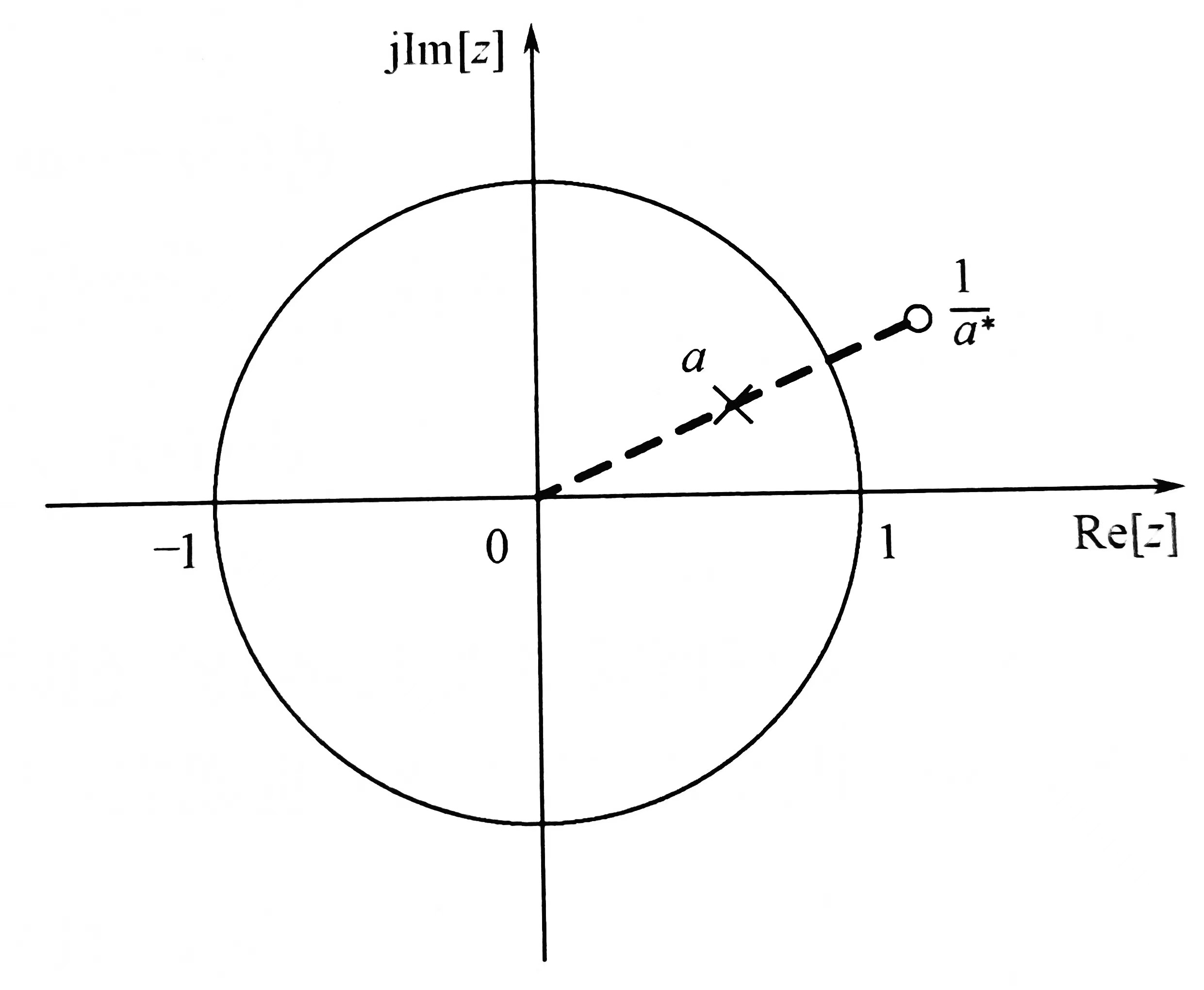
同理,可以推得全通系统映射到拉普拉斯变换的S域就是关于虚轴的镜像。
一个因果稳定的系统,其零极点都在单位圆内时,系统拥有最小的相位滞后,称为最小相移系统。这个定义虽然简单,但是没有那么直白:为什么零极点在单位圆内,相位滞后就最小了?这里,我们注意相位响应公式为:
\[arg[H(e^{j\omega } )]= arg[K]+\sum_{M}^{m=1} arg[e^{j\omega }-c_{m} ]-\sum_{N}^{k=1} arg[e^{j\omega }-d_{k} ]+(N-M)\omega\]其几何解释如图。注意\(c_{m}\)和\(d_{k}\)都是矢量,与矢量\(e^{j\omega }\)做差。
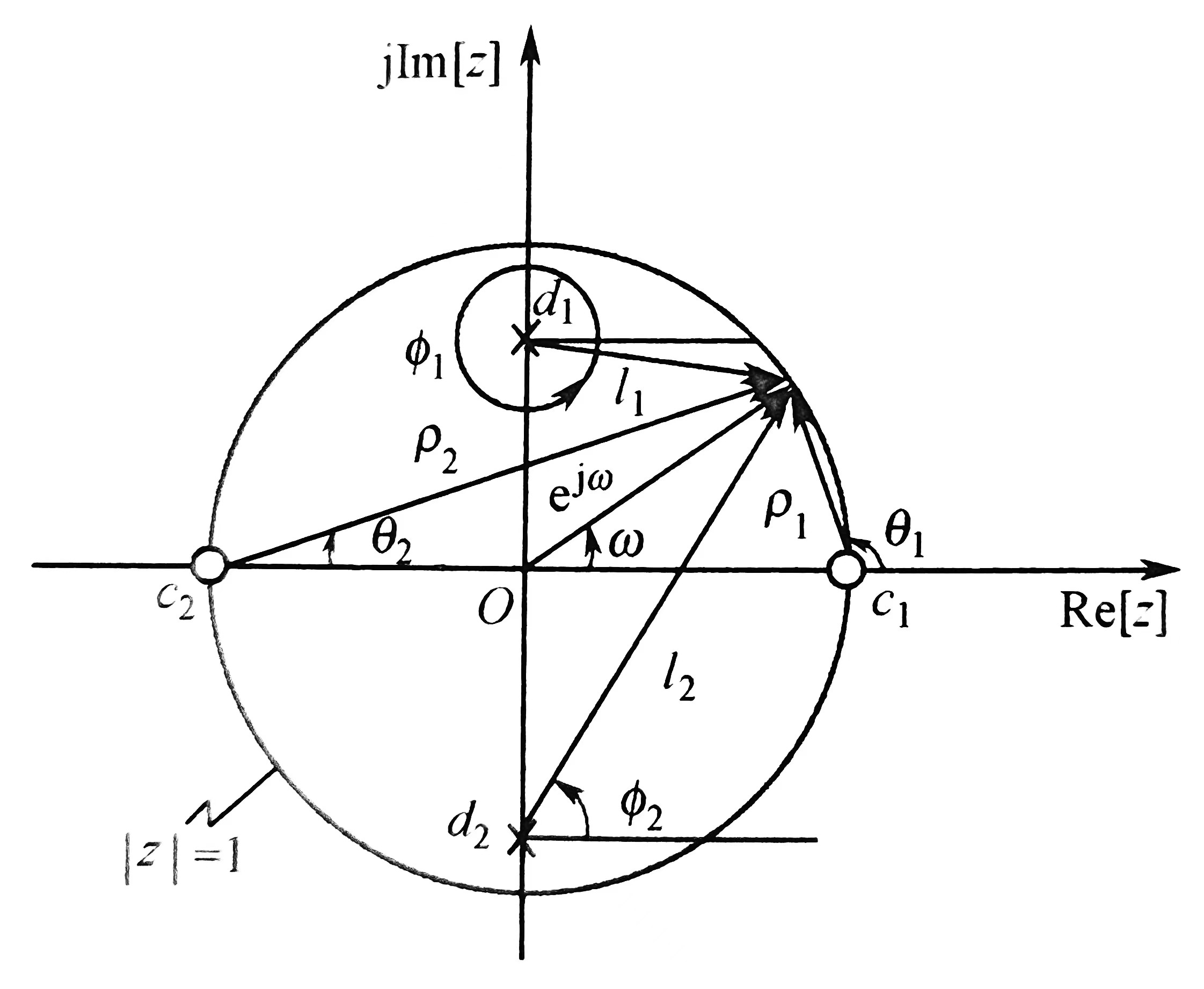
\(arg[K]\)项是常数,不对相位变化量\(\bigtriangleup arg[H(e^{j\omega } )]\)做贡献。此外,只要零极点在单位圆内,\(\omega\)每转过\(0\)到\(2\pi\),每个零极点都将产生\(2\pi\)的相位滞后。而因果系统所有极点都在单位圆内,所以极点N项正负抵消,只剩下零点项。同理,如果零点项也能正负相抵,\(\bigtriangleup arg[H(e^{j\omega } )]\)就可以取到最小值0,即零点全部在单位圆内就可以实现。
参考书籍:《数字信号处理》